跳转至

透视原理

分类

  • 线性透视：1，2，3点透视
  • 特殊透视：5点透视（效果上接近鱼眼透视），n点透视（无限多点为鱼眼透视）
  • 结构透视
  • 大气透视：近小远大，前后遮挡，透视变平，信息量减少

基本原理

近小远大，信息量减少

四大定理

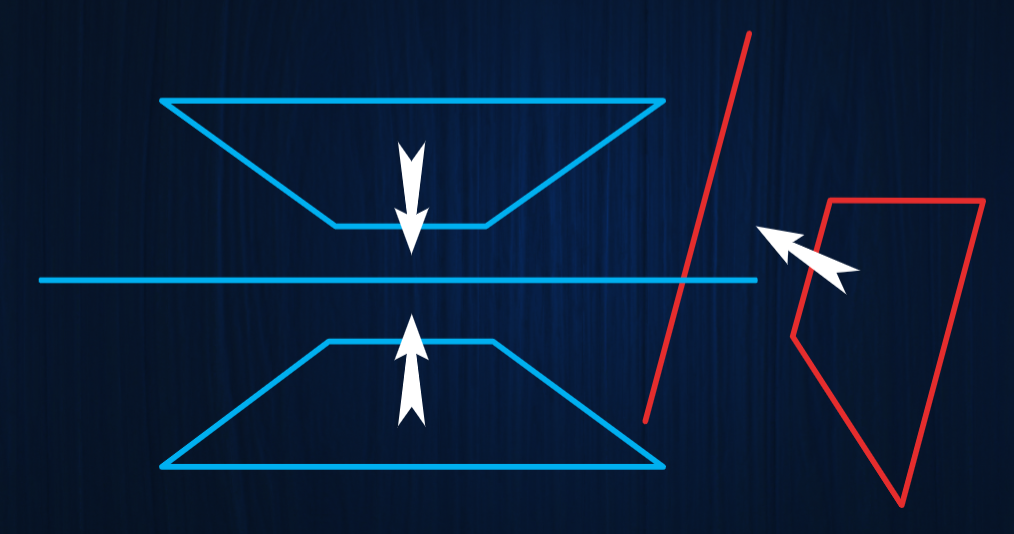
  • 平行的平面公用一条消失线，不平行的平面消失线不同

  • image-20220921210205023

  • 平行的直线消失于一点，不平行的直线消失于不同点

  • image-20220921210305710

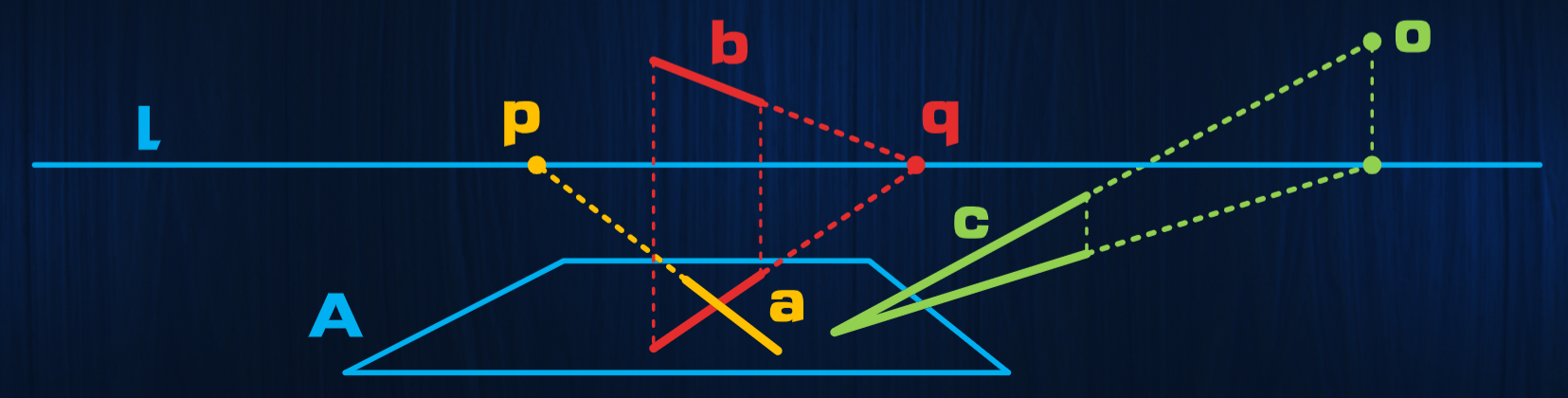
  • 平行于平面的直线的消失点位于该平面的消失线上（不平行于平面的直线的销失点不会位于该平面的消失线上）

  • image-20220921210444774

  • 垂直与视线的平面和直线不会发生透视变化（消失点或者消失线位于无穷远处）

视锥，视觉中心，视平面/视平线/视中线

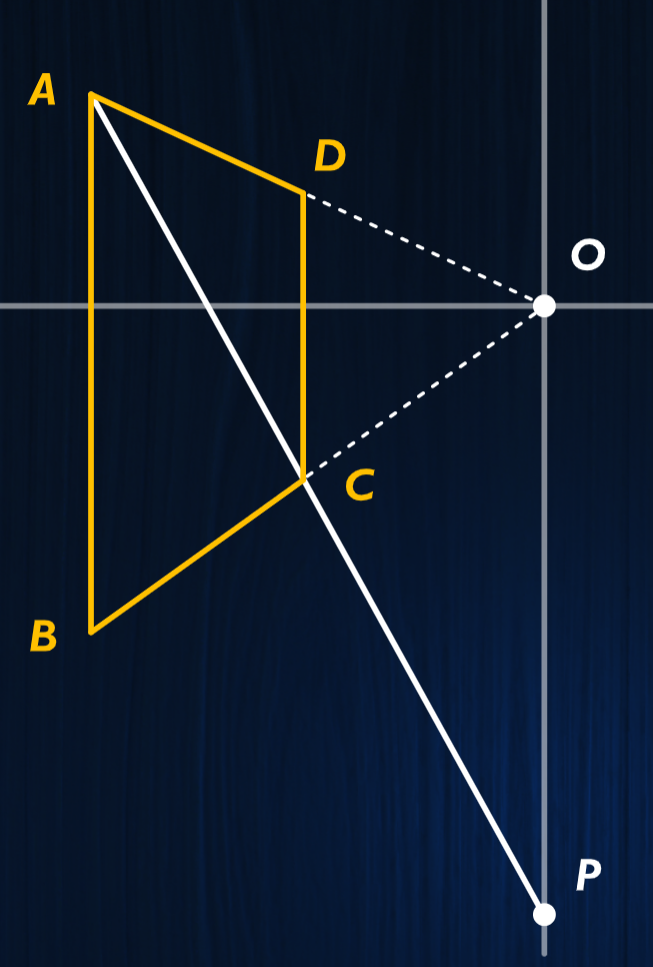
第五定理

经过观案点的直线与画面的交点即为该直线的销失点。 （同时也是空间中平行于该直线的所有直线的销失点） 经过观察点的平面与画面的交线即为该平面的消失线。 （同时也是空间中平行于该平面的所有平面的销失线）

使用方法: 将 视平面/视垂面 旋转至画布

image-20220922213653756

三大技法

实用技法

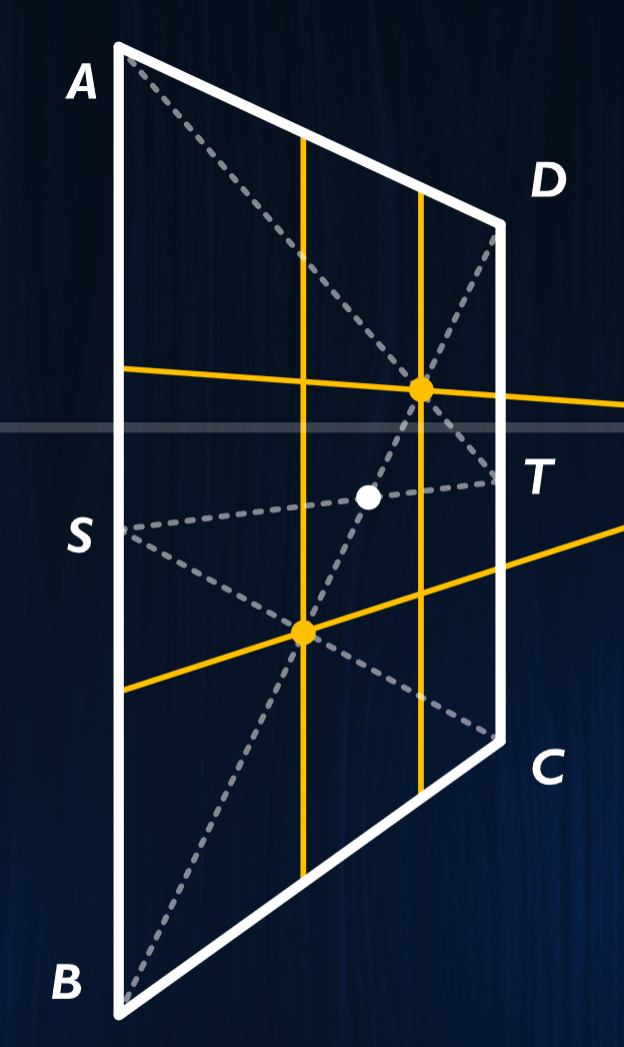
  • 等分法（X字法，三分法，，中心点，中心对称点，镜像对称点）

image-20220922212647210

  • 倍增法（N字法）

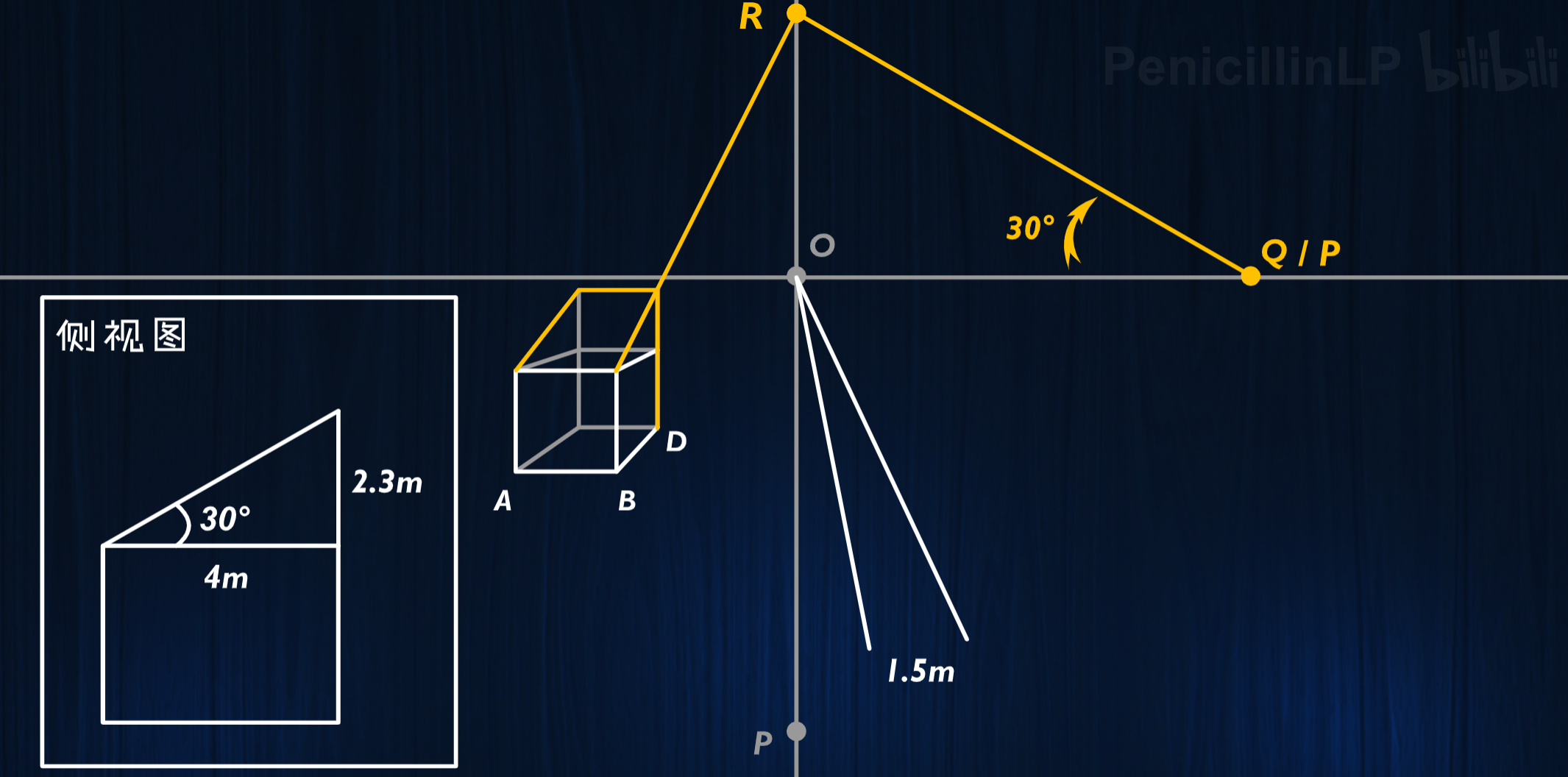
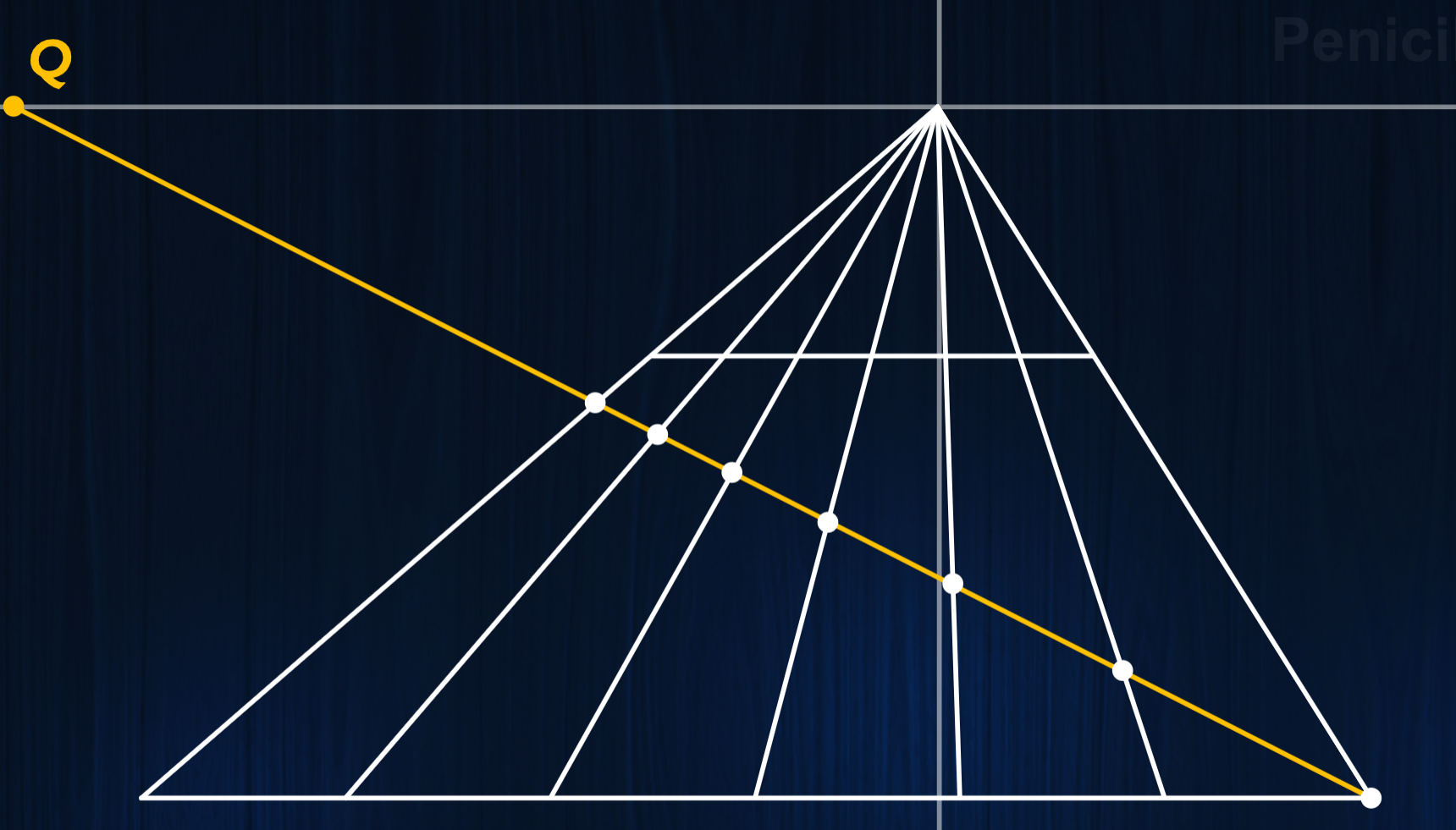
  • 任意切分伸缩（干净又卫生)(半角消失点P=Q)

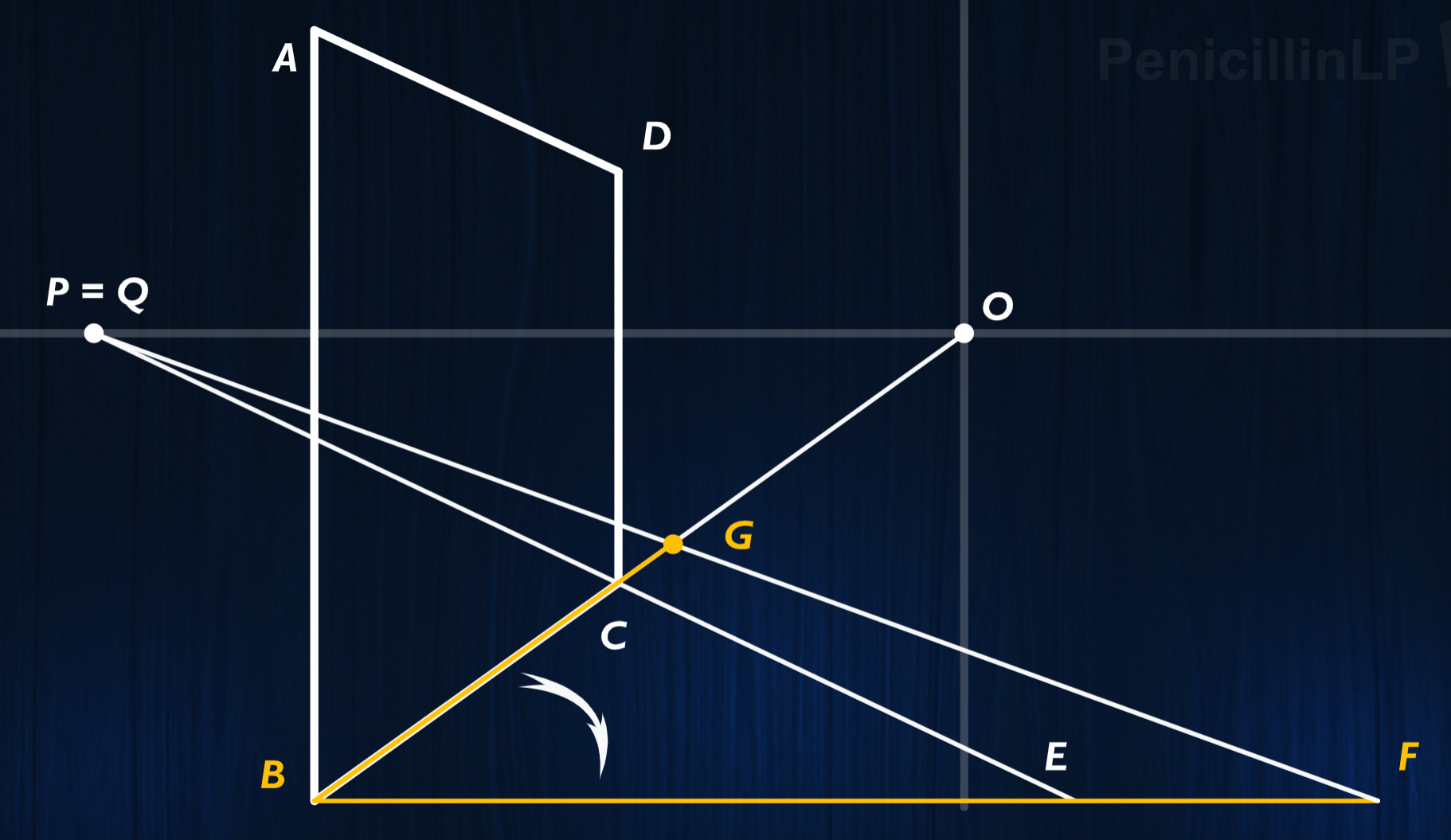
image-20220922212905863

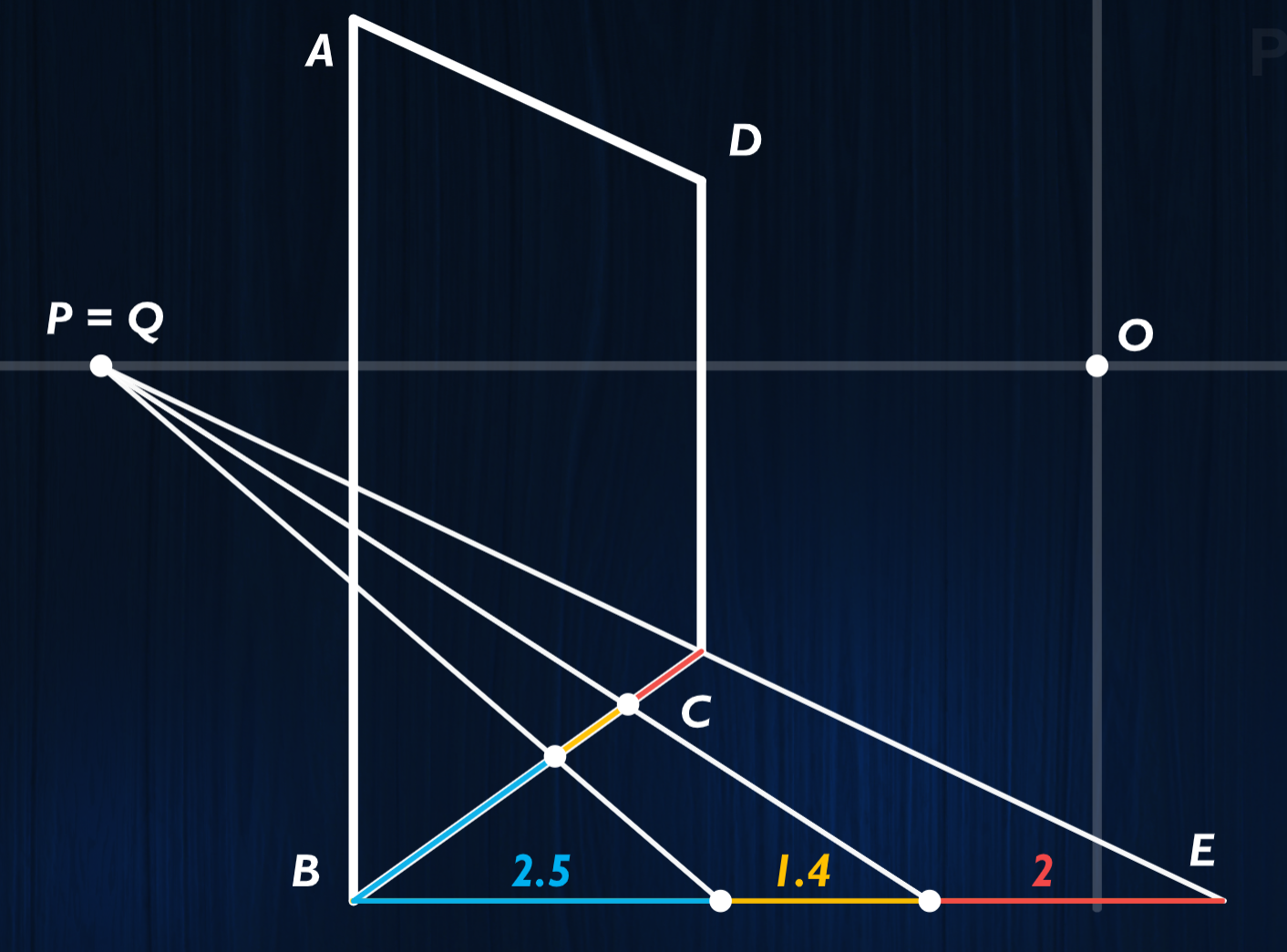
image-20220922212931312

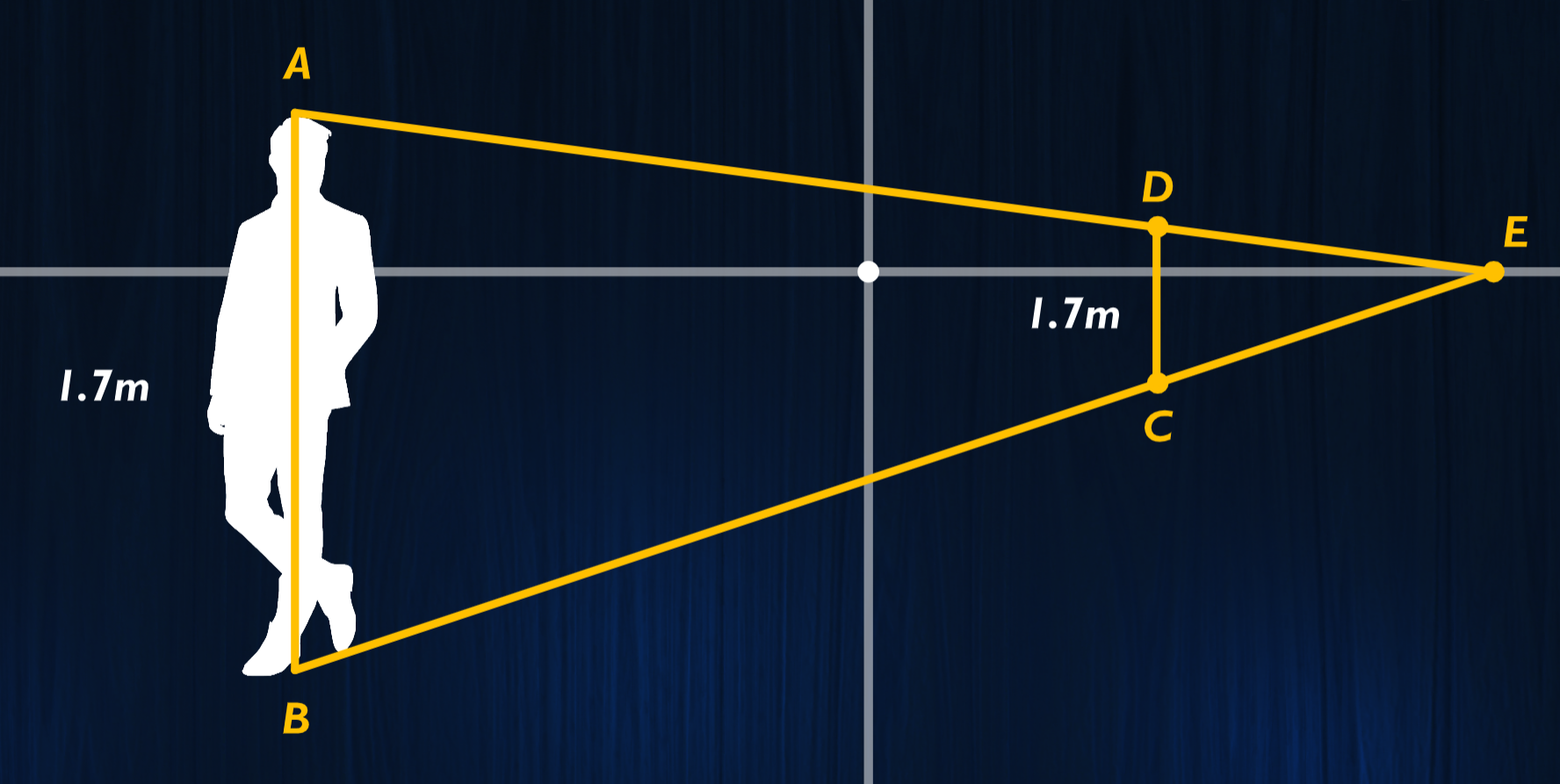
  • 同高度的人（极其位移伸缩）

image-20220922213104352

  • 绘制正方形网格

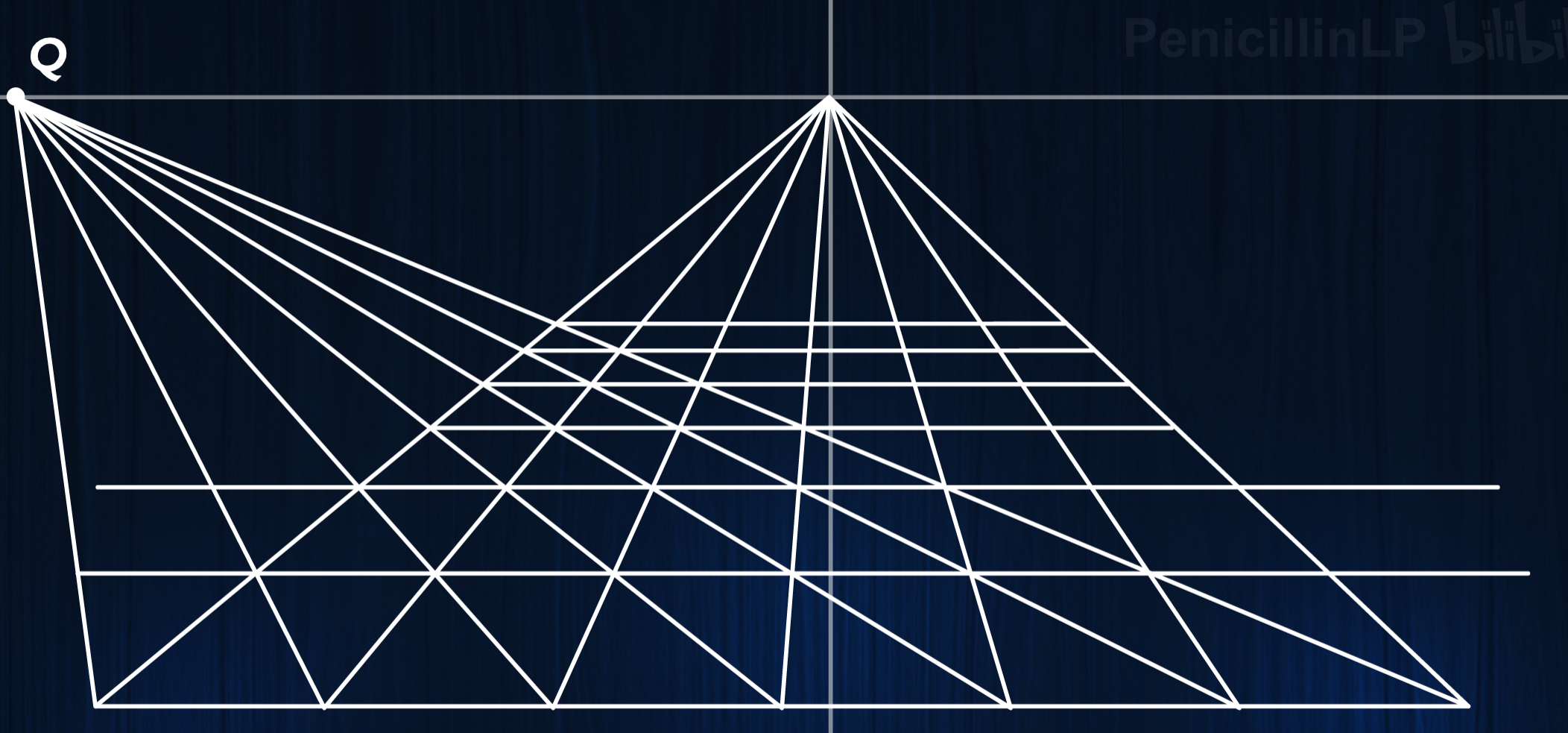
image-20220922213321202

image-20220922213353243

如何确定正方形

image-20220922212102053

如何选择观察点

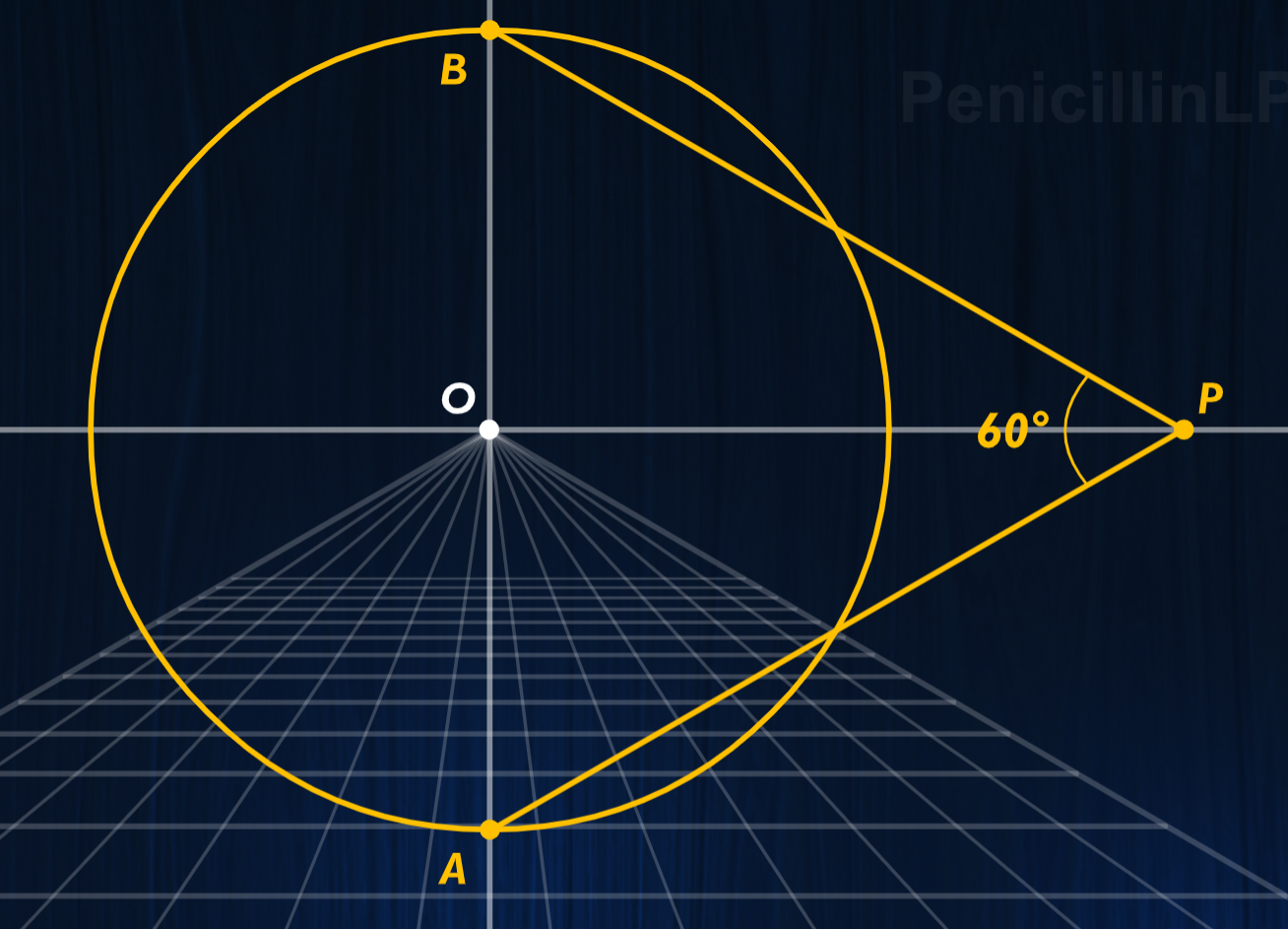
不同观察距离决定不同焦距（画布框与视锥/焦距相对大小）

常用视锥范围（60°）:透视畸变正常，超过了会渐渐畸变严重

image-20220922214215390

image-20220922214903713

使用例子：

古典一点透视位于视锥内

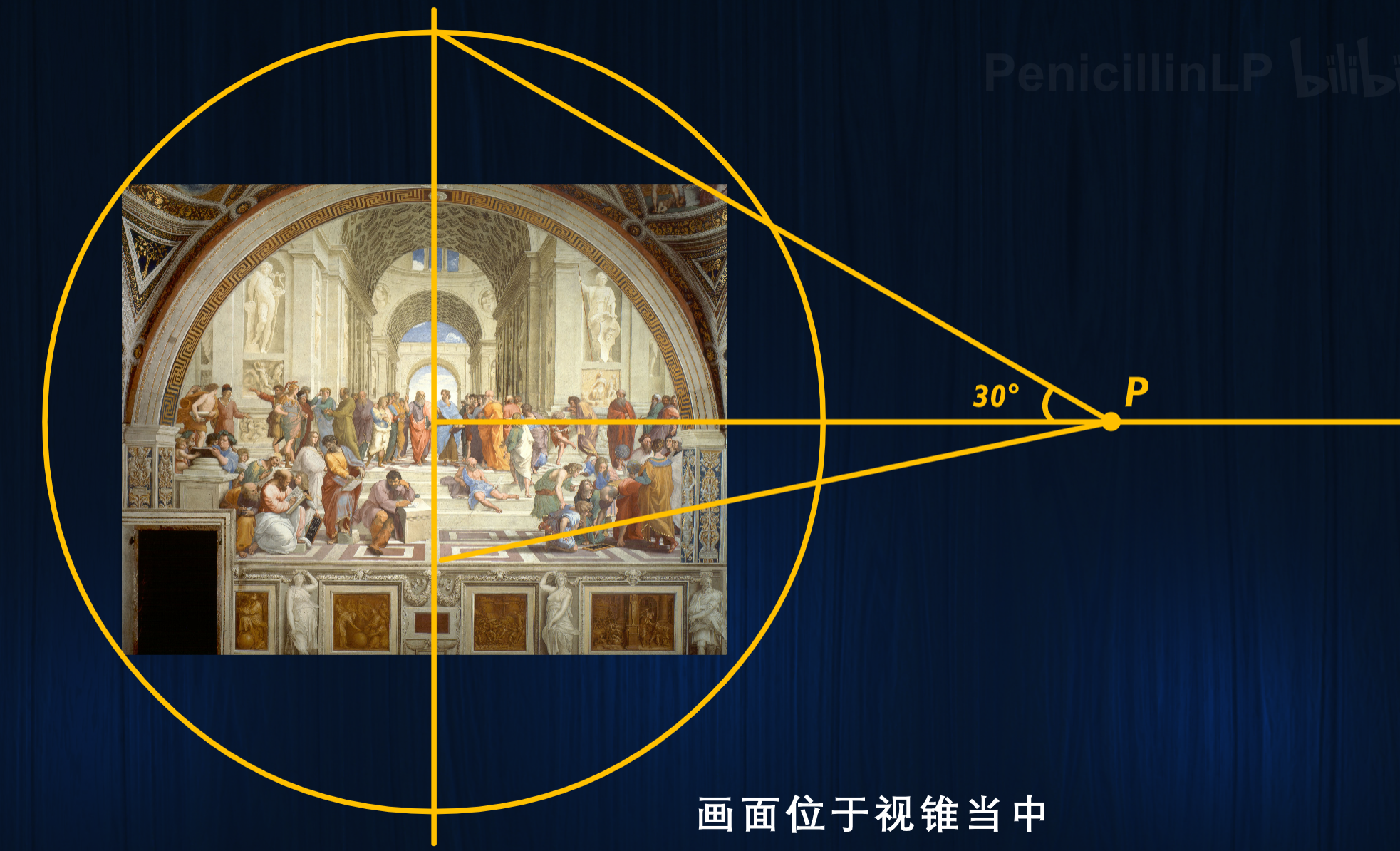
image-20220922215102527

故意创造透视畸变的效果

image-20220922215307957

image-20220922215326571

image-20220922215436415

思路：

image-20220922215542983

或者先画印象草图反推观测点&视锥

两点透视

半角消失点Q就是投射观测点P